西洋の歴史的な建築物には、しばしば「黄金比」が使用されているといわれています。ガウディのサクラダ・ファミリアも黄金比を取り入れていることで有名です。黄金比は1:1.618で表され、人が最も美しいと感じる比率として長年親しまれてきました。レオナルド・ダ・ヴィンチの作品にも黄金比が用いられていると推測されることが多く、映画化されたダン・ブラウンの小説『ダ・ヴィンチ・コード』でも、黄金比がストーリーの中で重要な役割を果たしています。

一方日本では、黄金比とは異なる1:1.414という比率が、古くから美しいとされる傾向にありました。この比率は、一般的に「白銀比」といわれ、法隆寺の五重塔や銀閣寺、近年では東京スカイツリーの設計にも採用されています。黄金比の1.618と白銀比の1.414は、どちらも無理数です。無理数とは分数の形で表せない実数のことで、小数点以下が無限に続きます。なぜこれらの特定の数値が、それぞれ黄金比や白銀比という美の代名詞として親しまれるようになったのでしょうか。この数値の背景や魅力について探ります。

数学における特別な比率「黄金比」とは？

黄金比について最初に言及したのは、古代ギリシアの数学者ユークリッドだといわれています。彼は著書『原論』で、ある線分を二つの部分に分ける特別な比率について記述しています。線分Aを二つの部分、BとCに分けた場合（Bの方が長いとする）、一般にA:Bの比とB:Cの比が同じになることはありません。例えば、もしBが全体の2/3、Cが1/3であるなら、A:Bは3:2、B:Cは2:1となり、これらの比率は異なります。しかし、ユークリッドは、この比率が同じになる点を見つけ出しました。これが約1.618:1だったのです。1.618……は、近代の数学者たちによってφ（ファイ）という記号で表されるようになりました。数学の授業で、円周率πが3.14159……であることは学びますが、φという数値があることまで学んだ人は限られているかもしれません。φは二乗すると、φ＋１と同じ数値になり（φ×φ＝φ＋1）、黄金比が数学的にも美しい数値であることを表しています。この比率は、芸術家や建築家にも長い間魅了され、19世紀には「黄金比」という名前で広く知られるようになりました。

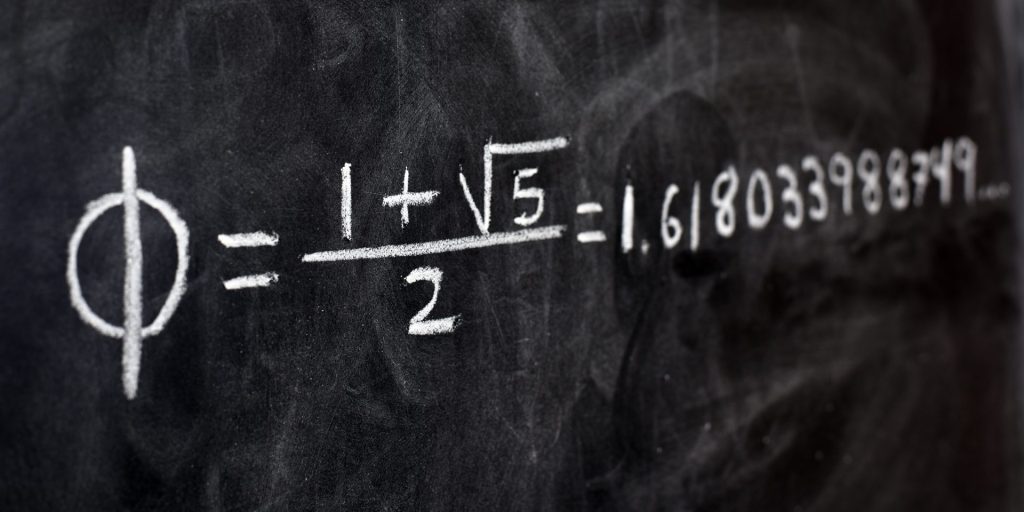
黄金比はどうして人を魅了するのか？

黄金比と密接に関連する数学的現象に、「フィボナッチ数列」があります。この数列は、0と1から始まり、次の項が常に前の2項の和となるように構成されており、「0, 1, 1, 2, 3, 5, 8, 13, 21, 34.……」と続きます。この数列において、「1:1、2:1、3:2……」のように隣接する数の比を求めると、最初は大きく変動しますが、数列が進むにつれて1.6180339887……であるφ（ファイ）、つまり黄金比に近づいていくのです。フィボナッチ数列は、自然界の多くの現象、例えばひまわりの種の配列や松かさのスパイラルパターンにも見られます。つまり、自然界の成長パターンや形成過程が、数学的に美しい黄金比に基づいていることを示唆しているのです。黄金比と自然界の調和が融合するのは不思議な感覚ですが、それこそが、人々が黄金比に魅せられる理由かもしれません。

黄金比が取り入れられた作品とは？

黄金比は、これまで多様な作品に影響を与えてきました。ルネサンス期のイタリアで活躍したルカ・パチョーリは、彼の著書で黄金比の数学的及び美学的側面を探究し、古代の建築やルネサンス絵画に美しい黄金比が見られることを示しています。著作内には、レオナルド・ダ・ヴィンチが描いた挿画が含まれており、黄金比が当時の芸術における重要な概念であったこともわかります。ダ・ヴィンチ自身の作品、例えば「モナ・リザ」や「最後の晩餐」にも、黄金比の使用が推測されており、同時代のミケランジェロやラファエロの作品にも黄金比が見られるとされています。彼らが実際に黄金比を用いたかどうかは確かではなく、未だに議論が続いています。しかし、それが偶然の一致である可能性も含め、人々が黄金比に親しみ、魅了されるきっかけになったといえるでしょう。

日本人に育まれてきた美学「白銀比」とは？

一方日本では、黄金比とは異なる白銀比が好まれてきました。白銀比の1.41421356……という数値は、見覚えがある人が多いかもしれません。「ひとよひとよにひとみごろ……」と覚えたあの数値「√2」の解です。√2は、二乗すると2になる数値のことで、一般には馴染みがないと思いがちです。しかし√2は、比較的簡単につくることができます。例えば正方形の折り紙を斜め半分に折って三角形をつくります。このときの三角形の斜面は、元の正方形の一辺の√2倍の長さになるのです。私たち日本には、折り紙のほかにも、風呂敷や枡など、正方形がたくさん存在します。畳2枚を横に並べた2畳分も正方形になり、平安京の区画も正方形だったといいます。

さらに、白銀比は日本独自の紙のサイズ規格であるB判にも見られます。B判の縦横比が白銀比に近いことから、この比率が日本の生活に深く浸透していることがわかります。中村滋著「フィボナッチ数の小宇宙」（日本評論社）によると、「日本人がどのような比率の四角形を好むのか」といった調査で、1位が白銀比に近く、2位が正方形、3位に黄金比に近い比率を選んだそうです。黄金比よりも、正方形や、正方形から導かれる白銀比に近い比率が上位にランクインするのは、正方形文化が息づく日本では自然なことかもしれません。

白銀比を生み出した日本独自の大工道具

日本に正方形が多いことは、丸い木材を無駄なく使うためだとする説があります。丸い木材を長方形ではなく、正方形にカットした方が最大面積になることは、数学でも証明できます。丸い木材から正方形を取り出す過程では、円の直径と正方形の対角線を一致させる計算が必要です。この過程で使われていたのが、日本独自の大工道具「曲尺（さしがね）」です。曲尺は長さが異なるものさしを直角につなげたような形をしています。曲尺には、表目にも裏目にも目盛りが記されています。表目は尺貫法の寸法通り（現在はcm）の目盛りですが、裏目はその目盛りを√２倍した数値が記されています。つまり、丸太の直径を裏目で測って目盛りを読めば、簡単に正方形の１辺の長さを求められるのです。日本では、この曲尺を用いてあらゆるものを測ってきました。この曲尺の存在が、日本の木造建築物における寸法取りの精度を高め、白銀比という美しい比率の実現を助けてきたのかもしれません。

現在も、白銀比や黄金比を取り入れた設計を実現するのに必要なのは正確な”はかる”技術。トプコンは1932年の創業以来、位置を精密に”はかる”技術で建設現場に貢献してきました。最新の技術が搭載された測量機器で、これからもトプコンは新しい創造の可能性を拡げていきます。

トプコン「測量の製品一覧」

（参考文献）

・創元社「黄金比　秘められた数の不思議」

・祥伝社「日本の美と心をつなぐ「白銀比」の謎　雪月花の数学」

・日経電子版「くらしの数字考　黄金比と白銀比、時空を超えて支持される理由 「かわいい」比率、日本に宿る　欧米と美の好みに差あり」